Questioni di gravità RKE03.2014

Questo articolo è nato un po’ per caso, da una innocente domanda fra amici: “ma gli astronauti sulla ISS, pesano soltanto meno o sono veramente in assenza di gravità?”

Il quesito, al di la di quanto la fisica che vedremo più avanti ci insegna, è istintivamente sostenuto dalla percezione di “galleggiamento” che abbiamo vedendo le immagini riprese a bordo della stazione spaziale, che ci inducono a pensare ad un ambiente privo di forze e pesi…

Per rispondere con sufficiente compiutezza ed al tempo stesso relativa semplicità alla domanda iniziale, vediamo un poco assieme di schematizzare la situazione ipotizzata.

Per semplicità di trattazione, consideriamo il nostro pianeta come una massa omogenea, di forma sferica e con un raggio di circa 6371km. In realtà, ben sappiamo che questa è una approssimazione, dato che la teorica sfera è schiacciata ai poli e le montagne ne rendono la superficie tormentata e di quota variabile e la sua densità è variabile da punto a punto. Ma per la precisione richiesta, vedremo come queste variabili, saranno assolutamente trascurabili ai fini del risultato…

La ISS, Stazione Spaziale Internazionale è un satellite posto in un’orbita terrestre quasi circolare. La sua altezza dal nostro pianeta è variata nel corso degli anni per vari motivi e per questo prenderemo per i nostri calcoli il valore di 347km come medio, con valori di apogeo e perigeo di 341 e 353km.
Se disegnassimo in scala Terra e ISS, vedremmo immediatamente, come nonostante 350km di quota ci sembrino tanti (e lo sono per chi ci deve andare, su un vettore!), di fatto l’orbita “sfiori” il nostro pianeta.

Per chi avesse bisogno a questo punto di una risposta rapida, esiste in letteratura una “formula magica” che calcola l’accelerazione gravitazionale terrestre in funzione della posizione e dell’altezza, che così recita:

g=9,7803184⋅(1+0,0053024⋅sin^2L−0,0000059⋅sin^2 2⋅L)−3,086⋅10−6⋅h(1)

dove: L è la latitudine (in gradi) e h è la quota (in metri) considerata.
Ora, trascurando l’effetto della latitudine (dovuto allo schiacciamento polare del nostro pianeta) e per una altezza di 347km, risulta:

gISS=9,7803184−3,086⋅10−6⋅347000≈8,71m/sec^2

Bene… già risolto il quesito? Forse.. ma siamo sicuri che la “formula magica” sia giusta??
Nel dubbio, perché non proviamo a trovare un modo “nostro”, trasparente, di calcolare la stessa grandezza?

Ecco, allora, semplifichiamo ancora il sistema ed immaginiamo la ISS come un punto nello spazio che corre su una circonferenza con centro il nostro pianeta.
La circonferenza (lunghezza dell’orbita) sarà dunque lunga:

s=2⋅π⋅(RaggioTerrestre+Altezzamedia)=2⋅3,14⋅(6371+347)≈42209km

Il periodo medio orbitale (giro completo intorno alla Terra) è oggi di 91’48” pari anche a 5508” (poco più di un’ora e mezza).

Bene, la ISS ed il suo equipaggio, viaggiano quindi alla rilevante velocità (rispetto alla Terra) di:

∣v∣=∣st∣=422095508≈7,66km/sec≈27587km/h!

Per successivi calcoli, può essere conveniente calcolare anche la velocità angolare:

ω=2⋅π5508≈0,00114rad/sec

Ora, val la pena mettere in evidenza, come il viaggio in orbita della stazione, non sia rettilineo, come su una ipotetica autostrada, ma in continua “curva”. Ogni momento cioè, cambia un poco la direzione del suo moto, pur rimanendo la sua velocità costante. Se così non fosse, la stazione partirebbe “per la tangente”, dritta come un fuso, perdendosi nello spazio…

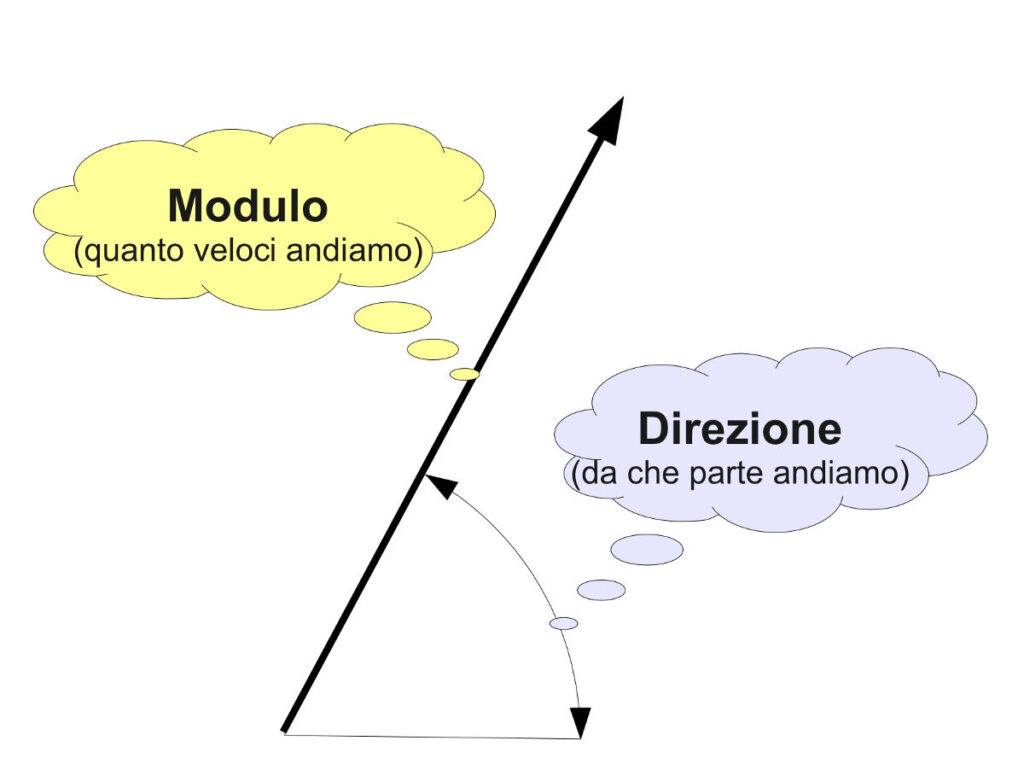
Ora, ritornando alle nostre basi di fisica, ricordiamo come la velocità sia un vettore, una grandezza cioè costituita (più o meno coscientemente nella vita quotidiana) da due componenti: un modulo (che ci dice quanto veloci andiamo) ed una direzione (che ci dice da che parte andiamo).

Ora, tutte le volte che la velocità cambia, sappiamo che possiamo parlare di accelerazione.
Nel nostro caso, è conveniente scomporre l’accelerazione in due componenti: una tangenziale ed una radiale, disposte come in figura sotto:

La componente perpendicolare alla traiettoria (accelerazione centripeta) quantifica il cambio di direzione del vettore velocità, mentre la componente tangente alla traiettoria quantifica la variazione del modulo del vettore velocità ed è detta accelerazione tangenziale. Il vettore accelerazione centripeta, quindi, per definizione, è in ogni istante perpendicolare al vettore velocità e non contribuisce alla variazione del modulo di quest’ultima, variazione che è invece legata all’accelerazione tangenziale.

Per il calcolo dell’accelerazione è conveniente usare la formula seguente:

a(t)=d/dt⋅(ω⋅r)

dove:
ω: è la velocità angolare
r: è il raggio della circonferenza

Per semplificare i calcoli e le successive deduzioni, scomponiamo il vettore complessivo dell’accelerazione nelle due già citate componenti tangenziale e centripeta:

a(t)=ac+at=ω⋅dr/dt+˙ω⋅r

Dato che l’orbita della nostra stazione è pressoché circolare e la velocità (o meglio il suo modulo) sostanzialmente costante, anche la sua derivata sarà nulla. Il secondo termine dell’equazione (accelerazione tangenziale) sarà dunque nullo e questo, forse, in fondo ce lo aspettavamo.
Concentriamoci dunque sul primo termine, quella accelerazione cioè che fa tenere al nostro satellite un’orbita circolare, facendolo “voltare” continuamente.
Semplificando un poco i conti si ottiene la seguente:

∣ac∣=ω2⋅r=0,001142⋅6718000≈8,74m/sec^2

quindi circa l’89% di quella mediamente misurabile qui, sulla Terra e molto prossima a quei 8,71m/sec^2 calcolati ad inizio dello studio.

Sulla ISS c’è eccome la forza di gravità, anche se un poco ridotta rispetto al suolo! E per fortuna che c’è! In caso contrario: bye, bye ISS, destinata a perdersi nello spazio…
La causa di quel continuo “piegare” della traiettoria è proprio l’interazione fra la massa della Terra e quella della stazione orbitante, che si manifesta in attrazione gravitazionale.
In termini esemplificativi, possiamo affermare che quando la tendenza di un corpo a “fuggire” da un altro è perfettamente bilanciata dalla forza con cui viene invece dallo stesso attratto, si realizza quella meravigliosa condizione di equilibrio che consente l’orbitare del primo rispetto al secondo, senza cadere e senza perdersi nel vuoto…

Quindi, tornando alla nostra domanda iniziale… il solito barattolo di Nutella che tutti gli astronauti si portano appresso quanto pesa una volta arrivati sulla stazione spaziale? Mah… a questo punto verrebbe da dire che peserebbe l’11% in meno che alla partenza… Eppure… se gli astronauti lo mettessero sul piatto della bilancia di casa che si sono portati in orbita… sorpresa:.. peserebbe zero!

Dove sta allora la verità?

Il problema sta nella domanda! Così come formulata in principio, sottintende una stretta relazione fra accelerazione di gravità e peso… Un fatto che sembra scontato per la comune esperienza ed umana percezione , mentre in determinate condizioni, le cose hanno diverso corso.

Dividiamo ora i due concetti: assenza di peso e assenza di gravità.

L’assenza di peso è la condizione che sperimenta un corpo in caduta libera. Il classico esempio è quello dell’ascensore che precipita. Al suo interno le persone percepiscono e misurano una totale assenza di peso… ma è chiaro a tutti che la gravità (e non solo della situazione) è presente. Il primo fisico che studiò il problema fu “tal” Newton che nella sua teoria della gravitazione, intuì come un osservatore solidale con l’oggetto in caduta libera non sia inerziale e le forze apparenti dovute alla non inerzialità del sistema di riferimento bilanciano la forza di gravità e la risultante (il peso) è nulla. In tempi più recenti (secolo scorso), questa prima formulazione fu rielaborata (specificamente dalla Relatività generale) incorporando il principio di equivalenza che asserisce come non sia possibile distinguere tra forze gravitazionali e forze apparenti. In altri termini, nella moderna descrizione relativistica la forza peso è essa stessa una forza apparente e l’osservatore inerziale è quello in caduta libera.

L’assenza di gravità invece è la condizione che si esprime con la mancanza totale di forze. E se andiam per il sottile.. è ben difficile da realizzare nell’universo! Due sole le condizioni che ci possono porre un questa situazione: una distanza “infinita” da altri corpi (per cui la loro attrazione si esaurisce) oppure essere ad una distanza opportuna da due o più corpi celesti tale che la somma delle loro attrazioni si annulli. Quest’ultimo è ad esempio il caso di un viaggiatore che si muovesse fra la Terra e la Luna. Giunto alla distanza di circa 339000 km dalla partenza, si troverebbe nel punto di equilibrio, “tirato” in egual misura da un lato, dal nostro pianeta, dall’altro, dal nostro satellite… in quel preciso momento sarebbe senza gravità! (trascurando quella del Sole e degli altri corpi celesti).

Quindi, peso ed accelerazione gravitazionale non sono la stessa cosa! Ecco perché la risposta alla domanda iniziale appare contraddittoria.

Questo chiarito, una interessante ed innocente domanda che potrebbe sorgere è quella che ci porta a chiedere come mai quando viaggiamo su un aereo di linea, che apparentemente segue una traiettoria simile a quella della ISS, non ci troviamo a galleggiare all’interno della fusoliera.
Una risposta sommaria sarebbe quella che afferma che volare e orbitare non sono la stessa cosa! Vero certamente.. ma in cosa si differenziano questi due modi di viaggiare? Proviamo a rispondere con semplicità.
Come anticipato e spiegato prima, la ISS così come un qualunque altro satellite, rimane nella sua traiettoria in quanto in ogni momento la sua velocità bilancia perfettamente la tendenza a cadere. Non così una velivolo di linea, che appunto “vola” e non precipita in quanto sostenuto da una differenza di pressione sulle superfici alari create dal loro particolare profilo e dalla velocità relativa rispetto all’aria. Se per fantasia togliessimo l’atmosfera terrestre, tutti i satelliti rimarrebbero al loro posto mentre nessun aereo odierno potrebbe nemmeno alzarsi da terra, a prescindere dal motore impiegato. Se volessimo trasformare un aereo in un oggetto orbitante, capace cioè di perpetuare la propria traiettoria attorno al nostro pianeta a prescindere dall’atmosfera e da fenomeni aerodinamici dovremmo inventare un qualche mezzo per portarlo alla velocità di circa:

Vplane=√mTerra⋅Graggioorbita≈√5,9736⋅1024⋅6,67⋅10−11(6371+10)≈7,899km/sec≈28438km/h

per una quota tipica di 33000piedi, equivalenti a circa 10000m.
La velocità media di un volo di linea è oggi circa 800km/h, circa 1/35 di quella necessaria ad orbitare! E’ proprio questa mancanza di velocità e quindi di lontananza dalla situazione di equilibrio che caratterizza un’orbita chiusa, a non farci percepire una significativa diminuzione di peso..

Finisco con una piacevole chiosa… ma come si calcola il punto di equilibrio nel viaggio dalla Terra alla Luna?
Riprendiamo alcuni concetti di base della fisica e vediamo come usarli per risolvere il nostro problema.
La forza gravitazione che attrae due corpi è descritta dalla nota formula:

F2,1(r)=G⋅m1⋅m2/r^2

dove m1 e m2 sono le masse dei due corpi considerati, r la distanza che separa il loro baricentri e G la costante di gravitazione universale che vale circa 6,67 × 10-11 Nm²kg-2
Ricordando ora che:

a=F/m

dividendo ambi i membri per m2, è possibile riscriverla, mettendo in evidenza l’andamento dell’accelerazione gravitazionale come segue:

ag=G⋅m1/r^2

Dalla formula si evince come l’interazione si annulli asintoticamente solo a distanza infinita e con un decremento quadratico.
La formula (1) non è quindi utilizzabile (in questo caso) dato che fa corrispondere gravità zero ad una distanza di soli:

r=9,783/,086E−3≈3169km

e per di più con una riduzione lineare al crescere della distanza.

Altro risultato delle “formule magiche”:.. diffidare.. o per lo meno chiedersi sempre a quali condizioni danno risultati corretti.

Ora, tornando al nostro quesito e pensando all’ipotetico viaggiatore dalla Terra alla Luna, possiamo prevedere l’andamento dell’accelerazione gravitazione a cui sarà sottoposto scrivendo:

a(r)=G⋅MTerra/r^2−G⋅MLuna/(D−r)^2

dove:
a(r) è l’accelerazione gravitazionale lungo la traiettoria geodetica fra il centro della Terra e quello lunare
MTerra: massa terrestre, pari a circa 5,9736*1024 kg
r: distanza dell’astronauta dal centro della Terra
D: distanza media fra i baricentri di Terra e Luna, circa 384000km
MLuna: massa lunare, circa 7,3477*1022 kg
Mettendo in forma grafica la soluzione dell’equazione si ottiene:

Conclusioni: partendo da una innocente domanda, abbiamo esplorato velocemente il mondo dei corpi orbitanti e quanto a loro accade. Mi perdoneranno i più esperti per il linguaggio “popolare” e le varie semplificazioni adottate, ma scopo dello scritto non era uno studio di dettaglio quanto provare con mezzi semplici a ragionare su alcuni temi e a vedere le cose, magari in modo un poco diverso..
Buona gravità a tutti..

Bibliografia
spaceports.blogspot.com/2009/03/soyuz-on-way-to-iss.html
it.wikipedia.org/wiki/Punti_di_Lagrange
it.wikipedia.org/wiki/Accelerazione_di_gravit%C3%A0
astro1.phys.uniroma1.it/tacor/remote_lab/luna.pdf