The Albis capacitor RKE03.2010

The strange Albis’s capacitor….

Capita che un giorno passo da Torino e vado a pranzo col nostro direttore, Gianfranco… Chiacchiera dopo chiacchiera davanti alla sua collezione di strumenti antichi, salta fuori uno strano condensatore variabile, “quadrato”… in cui le facce di forma triangolare si inseriscono le une nelle altre frontalmente.

Una domanda nacque spontanea: perché mai l’avranno fatto in questo strano e complicato modo?

Ecco che allora nasce l’opportunità di riprendere in mano i quaderni di scuola e fare un po’ di ripasso delle formule base dell’elettrotecnica..

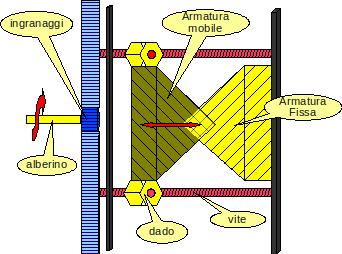
Anzitutto vediamo le parti base del componente marchiato come: WADE TYPE A 0.0005 MFD MADE IN USA TRADE MARK PATS. PNDG.

Ruotando l’alberino, tramite alcune ruote dentate e un sistema a doppia vite si mette in traslazione il gruppo di lamelle mobile. La sovrapposizione delle stesse con quelle fisse ha una forma romboidale con un rapporto fra le diagonali costante.

Definito il sistema, cominciamo il ripasso delle formule..

Poniamo:

d = spaziature armature

S = area affacciata armature

l = avanzamento armature (diagonale minore del rombo)

r= rapporto fra le diagonali dei rombi (armature)

α = angolo rotazione manopola

k1 = coefficiente proporzionalità angolo manopola/avanzamento armature

C = capacità del condensatore

ε = costante dielettrica assoluta

n = numero delle lamine

iniziamo a calcolare la sovrapposizione delle lamine azionando l’alberino di comando:

[1]

data la particolare geometria costruttiva del condensatore (in cui le facce si inseriscono le une nelle altre lungo la diagonale), la superficie totale affacciata vale:

 [2]

ricordiamo ora, il caso generale di un condensatore a facce piane e parallele, la cui capacità è calcolata come:

sostituendo ora alla generica superficie “S”, quella del nostro condensatore, sopra identificata nella formula [2] si ottiene:

e poi sostituendo a “l”, profondità di penetrazione delle lamine, la sua relazione con l’angolo della manopola, descritta dalla [1] si ha:

radunando i termini si ottiene:

[3]

per semplificare un po’ la scrittura, possiamo radunare tutti i termini costanti del problema in un nuovo coefficiente che chiameremo k2:

quindi, possiamo riscrivere la [3] in forma molto più compatta come:

[4]

in termini pratici, questo esprime il fatto che il valore di capacità è proporzionale al quadrato dell’angolo di rotazione della manopola e questo è il primo risultato che cercavamo.

Per meglio evidenziare il “carattere” della legge di variazione proviamo ora a derivare (cioè calcolare il rapporto fra variazione d’angolo manopola e variazioni di capacità) la funzione rispetto all’angolo, ottenendo:

da cui si evince con maggiore chiarezza come la variazione di capacità sia direttamente proporzionale alla posizione.

Facciamo due esempi:

• partendo da zero angolo e capacità, se con una rotazione di un giro ottengo 100 pF, con due giri avrò 400pF e a metà del primo solo 25 pF.

• se dopo un giro, un grado di rotazione di manopola varia del 2% la capacità, al secondo giro, la stessa rotazione provocherà una variazione del 4%.

Bene, trovata la legge di variazione, cerchiamo di intuire quale ne potesse essere l’utilità.

Proviamo ad esempio a vedere cosa succederebbe quando si impiegasse detto condensatore variabile in un circuito risonante LC.

La formula generale della pulsazione di risonanza è:

per chi è più avvezzo a parlare di frequenza piuttosto che di pulsazione, ricordiamo che la relazione fra le due vale:

sostituiamo ora alla generica C (capacità) la sua espressione [4] funzione della rotazione manopola prima ricavata si ottiene:

semplificando e portando fuori radice si ottiene:

 [5]

per semplificare un poco la scrittura, possiamo di nuovo creare una costante così definita:

e sostituendo nella [5], si ottiene:

cioè la pulsazione (o frequenza) di risonanza è inversamente proporzionale all’angolo della manopola. Proviamo ora ad immaginare questo circuito risonante come parte di un ricevitore…. ad esempio nell’oscillatore locale.

La relazione che lega, nello spazio libero, frequenza e lunghezza d’onda di una radiazione elettromagnetica vale:

dove F è la frequenza, λ la lunghezza d’onda e C la velocità della luce nel vuoto.

Riutilizzando le espressioni prima trovate, vediamo che succederebbe…

…“rimescolando” un poco i fattori e risolvendo per mettere in evidenza la relazione fra lunghezza d’onda e rotazione dell’albero del condensatore si ottiene:

…come a dire, che se graduiamo la scala della manopola in lunghezza d’onda (come si usava nei vecchi ricevitori)… la scala sarà lineare! …con innegabili vantaggi per il progettista dell’apparato.

Ma sarà poi vero tutto questo? Ecco che allora, dopo una pagina di calcoli, arriva il momento delle misure.

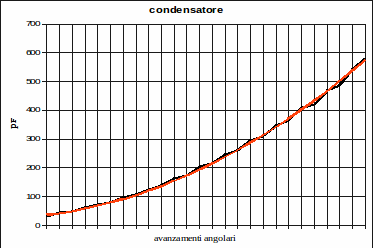
Con un po’ di pazienza, Gianfranco ha rilevato la capacità reale del condensatore ad intervalli di rotazione costanti, ottenendo la seguente tabellina:

Ora, per evidenziare il legame fra angolo e capacità reale, ipotizziamo una relazione del tipo:

che altro non è se non la generica equazione di una curva di secondo grado, con i consueti coefficienti a, b, c.

Facendo girare un algoritmo di “best fitting”, è possibile trovare la tripletta di a, b, c che meglio fa “ricopiare” all’equazione generica la curva rilevata sperimentalmente.

I coefficienti trovati sono:

a = 32

b = 4

c = 0,65

che come visibile nel grafico a fianco, ben descrivono la curva sperimentale.

Come senso fisico, “a” descrive la capacità residua del condensatore cioè la minima ottenibile a armature tutte aperte. Il coefficiente “c”, è il “k2” sopra impiegato che lega quadraticamente capacità e rotazione. Il termine di primo ordine, “b”, è la “differenza” fra la teoria dei calcoli e la realtà.. in altre parole condensa in se tutte le semplificazioni di calcolo prima impiegate, prima fra tutte l’omissione delle capacità parassite del sistema.

Bene, siamo arrivati in fondo e siamo soddisfatti di aver dato una spiegazione plausibile al quesito originale. L’auspicio è quello di aver unito alla curiosità su un vecchio componente l’occasione di un piacevole ripasso dei quaderni di scuola..